Hello! So this semester has been a fairly busy one for me and so I have not made much time to get anything new written.. until now!
Lately I've been having some real fun with optimization, especially convex optimization and some duality, but I recently got posed an interesting problem of bounding the error between an iterate and the local minimum for a quadratic form when using an approximate gradient instead of an exact one. I thought this was a fairly fun problem to investigate and thought I would share my proof and some numerical results! So let's get to it..

First, let us take a look at the recursive gradient descent approach in question. Consider the steepest descent method with bounded error:$\newcommand{\norm}[1]{\left \lVert #1 \right \rVert}$ $\newcommand{\Real}{\mathbb{R}}$
\begin{align*}
x_{k+1} &= x_k - s \left( \nabla f(x_k) + \epsilon_k\right)
\end{align*}
where $s$ is a positive constant stepsize, $\epsilon_k$ is an error term satisfying $\norm{\epsilon_k} \leq \delta$ for all non-negative integers $k$, and $f$ is the positive definite quadratic form defined as
\begin{align*}
f(x) = \frac{1}{2} (x - x^*)^T Q (x - x^*)
\end{align*}
We will also let $q = \max \lbrace|1 - s \lambda_{min}(Q)|,|1 - s \lambda_{max}(Q)| \rbrace$. With these definitions, we will aim to prove the following main result:
Main Theorem
If $q < 1$, then under the gradient descent sequence above with bounded error, we have that
\begin{align*} \norm{x_k - x^*} \leq \frac{s \delta}{1 - q} + q^k \norm{x_0 - x^*} \end{align*}
where $x_0$ is the starting point for the iterate sequence and $x^*$ is the local optima.
To end up with this main theorem, we will first prove some useful lemmas. To this end, we start with the first lemma.
Lemma 1
Given a value $0 \leq c < 1$ and that \begin{align*} \norm{x_{k+1} - x^*} \leq s \delta + c \norm{x_k - x^*} \end{align*} we can find a bound for $\norm{x_k - x^*}$ to be \begin{align*} \norm{x_{k} - x^*} \leq \frac{s \delta}{1 - c} + c^k \norm{x_0 - x^*} \end{align*}
\begin{align*}
\norm{ x_{k} - x^* } &\leq s \delta + c \norm{ x_{k-1} - x^* } \\
&\leq \left(1 + c\right)s \delta + c^2 \norm{ x_{k-2} - x^* } \\
&\;\;\vdots \\
&\leq \left(\sum_{i=0}^{k} c^i\right) s \delta + c^{k} \norm{ x_{0} - x^* } \\
&\leq \left(\sum_{i=0}^{\infty} c^i\right) s \delta + c^{k} \norm{ x_{0} - x^* } \\
&= \frac{s \delta}{1-c} + c^{k} \norm{ x_{0} - x^* } \\
\end{align*}
Lemma 2
For some symmetric, positive definite matrix $A$ and positive scalar $s$, the following is true:
\begin{align*}
\norm{I - s A} &\leq \max \lbrace |1 - s \lambda_{min}(A)|, |1 - s \lambda_{max}(A)|\rbrace
\end{align*}
Recall that some positive definite matrix $A = U^T \Lambda U \in \Real^{n \times n}$ where $U$ is a unitary matrix of eigenvectors and $\Lambda$ is a diagonal matrix with positive eigenvalues. Recall as well that for a matrix 2-norm, $\norm{B} = \sqrt{\lambda_{max}(B^T B)}$ for some matrix $B$. With that, we can proceed with the proof.
\begin{align*}
\norm{ I - s A } &= \norm{U^T U - s U^T \Lambda U} \\
&= \norm{U^T \left(I - s \Lambda \right)U} \\
&\leq \norm{U^T} \norm{I - s \Lambda} \norm{U} \\
&= \norm{I - s \Lambda} \\
&= \sqrt{\max \lbrace (1 - s \lambda_1)^2, \cdots, (1 - s \lambda_n)^2\rbrace} \\
&= \max \lbrace |1 - s \lambda_1|, |1 - s \lambda_2|\cdots, |1 - s \lambda_n|\rbrace \\
&= \max \lbrace |1 - s \lambda_{min}(A)|, |1 - s \lambda_{max}(A)|\rbrace
\end{align*}
Proof of Main Theorem
Our goal in this proof is to arrive at the end result by arriving at statements that allow us to benefit from Lemma 1 and Lemma 2. With that said, we can proceed with this proof as follows:
\begin{align*}
\norm{x_{k+1} - x^*} &= \norm{\left(x_k - x^*\right) - s \left(\nabla f(x_k) + \epsilon_k\right)} \\
&= \norm{\left(x_k - x^*\right) - s \left(Q \left(x_k - x^*\right) + \epsilon_k\right)} \\
&= \norm{\left(I - s Q\right)\left(x_k - x^*\right) - s \epsilon_k } \\
&\leq \norm{\left(I - s Q\right)\left(x_k - x^*\right)} + s \norm{\epsilon_k} \\
&\leq \norm{ I - s Q }\norm{ x_k - x^* } + s \delta \\
&\leq \max\lbrace |1 - s \lambda_{max}(Q)|,|1 - s \lambda_{min}(Q)|\rbrace \norm{ x_k - x^* } + s \delta \\
&= q \norm{ x_k - x^* } + s \delta \\
\end{align*}
Since we assume we choose $s$ to be small enough such that $q < 1$, we can use Lemma 1 to further show that \begin{align*} \norm{x_{k+1} - x^*} &\leq q \norm{ x_k - x^* } + s \delta \\ &\leq \frac{s \delta}{1-q} + q^{k+1} \norm{ x_{0} - x^* } \end{align*} Thus showing the result we want!
Numerical Methods
I thought it could be cool to do a numerical experiment to see how the bound compares to the convergence in practice. To do this experiment, a noise vector $\epsilon$ was added onto the exact gradient of the quadratic form for a random, positive definite $Q$ such that $\left \lVert \epsilon \right \rVert \leq \delta$ for some $\delta$ that is specified. Multiple sequences were run with different starting random seeds and the plot below is a visualization of the convergence results against the bound.
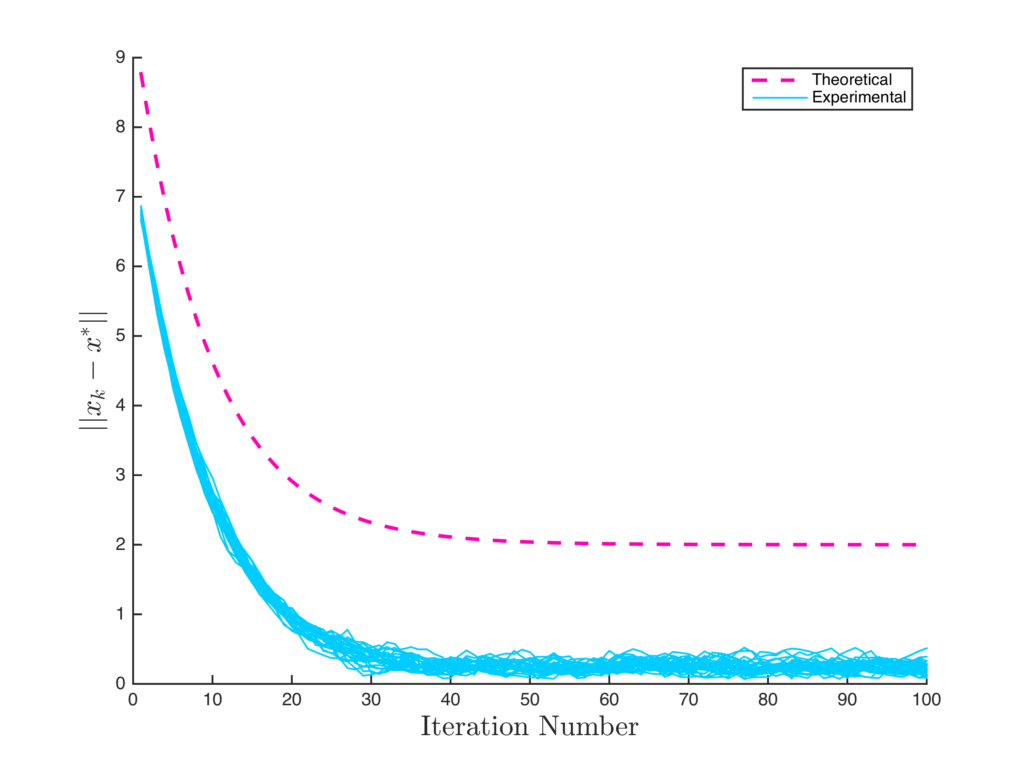
Based on the figure above, it looks like the bound works out nicely! Some observations to note are the following. As $q \rightarrow 1$, the bound term independent of $k$ in the inequality becomes quite large and the convergence of the $q^k$ term to $0$ slows down. This implies that the spectrum of $s Q$ are within a unit ball centered around a value of $1$ and that the extreme values of $s \lambda_{min}$ and $s \lambda_{max}$ are near the boundary of this ball. $q \rightarrow 1$ also means we are approaching a situation where we will diverge as the number of iterations approach infinity, so it makes sense that things would be bounded more and converge more slowly when $q$ is close to $1$.
Conclusion
In any event, we have seen that if we approximate our gradient in a way that is bounded (say using Finite Differences or mini-batch estimates in Machine Learning), it is possible to bound our convergence error and get a clearer idea of what to expect in terms of run-time, long term accuracy, and potentially more! Thus, this is a pretty neat result and something to keep in mind!


