In the modern climate of big data, it should not surprise anyone that we can be handed a dataset that is much too large to fit onto our personal computer’s hard drive, let alone having the dataset all load into RAM. Yet, these limitations do not stop us from trying to crunch bigger datasets and harvest even more data! 

With such a data abundance, how do we construct efficient algorithms to handle the limitations of our hardware? Depending on the sort of things you wish to compute with the data, the techniques one might use can be extensive. One direction to achieve this using low extra memory is by the construction of streaming algorithms. This topic will be the focus of this post, so let’s get rolling!

Basic Streaming Algorithm Concepts

So one might ask, what is a streaming algorithm? To start, let us consider what a stream might be. A stream could be viewed as a sequence of information that we iterate through until we hit the end of the sequence, if there is an end. In some contexts, one can only pass through a stream once while in other contexts one pass through the stream as many times as needed.

A streaming algorithm generally corresponds to an algorithm that operates on a stream to compute or estimate some quantity. Often, streaming algorithms operate on the assumption that the stream has so much data within it that algorithms operating on the stream should use a logarithmic or constant amount of added space relative to the stream size $n$. As an example, consider wanting to estimate regression parameters for some model dependent on a $1$ terabyte (TB) file of regression data. It becomes clear that having an algorithm that uses much less than $1$ TB of space to run would be very useful to tackling such a problem. Thus, streaming algorithms can be extremely useful!

Searching for a needle in a haystack

To solidify the idea of a streaming algorithm, we are going to dive into tackling the following problem:

Suppose we are given a stream $S = (s_1, s_2, \cdots, s_n)$ of size $n$ where each variable $s_i$ corresponds to real number. We are then told that there exists a unique number that appears at least $X$ times in the stream. Describe an algorithm that can find this unique number and describe the number of passes this algorithm requires through the stream of data, given you are handed the value $X$.

This problem came up recently in a discussion with a colleague and I felt it was interesting enough to try and find my own solution for. The rest of this post will go over some algorithms that solve this problem, the first being a pretty obvious deterministic algorithm and the second being a fun one making use of randomness.

The Naive Algorithm

Before we get to the more interesting algorithm, let us consider what might be viewed as the more naive algorithm to handle this problem. First, define $n_X$ as the desired number that shows up at least $X$ times in the stream. The main idea of the algorithm is going to be deterministically looping over the stream, where at iteration $i$ we set the $i^{th}$ value $s_i$ as a representative and then loop over the stream $S$ and count the number of times this number appears. If this number appears at least $X$ times, we know we have found the desired number $n_X$ and we can terminate. Otherwise, we increment $i$ and continue our search. The explicit pseudocode for this algorithm is defined below.

Some Analysis

It is pretty clear that this algorithm has us trying every type of number in the stream and seeing if its frequency is at least $X$, implying we will eventually find our desired number $n_X$ since it exists. Since for each value of $i$ we have to pass through the stream $2$ times, once to get the $i^{th}$ number as a representative and once to compute the frequency of that number, this implies in the worst case we will loop over the stream at most $2(n-X+1) \leq 2n$ times. Further, we can see that the only extra space we use other than the inputs is a few counters and a temporary number representing the representative. This implies our space complexity is at most $O(\log(n))$ bits. So this algorithm is simple, correct, and has a small space footprint!

A Randomized Algorithm

The previous algorithm is what we would consider deterministic, meaning that for the same input the algorithm will return the same answer in the same amount of runtime. In this case, we will consider a Las Vegas styled randomized algorithm, meaning for the same input the algorithm will return the same answer but its runtime can vary. This algorithm is going to be very similar to the previous one, but the twist leads to some interesting results.

At the start of this algorithm, on input of the stream $S$ and the value $X$, we will enter a loop that only ends if we find a representative $r$ from the stream that appears at least $X$ times in the stream. Within each loop iteration, we will pass through the stream once and uniformly at random choose a representative $r$ from the stream. From here, like the naive algorithm, we will reset the stream and loop through it and count how many times the representative $r$ appears. If the counter returns a value at least as large as $X$, then we know we are done. The key differences between this algorithm and the previous one is how we select the representative and how the loop terminates. In this case we could run forever while the naive algorithm has at most $n$ iterations of the main loop. The explicit algorithm details are listed below.

Now before going into the analysis of the above algorithm, how can we select a representative uniformly at random from the stream? Well one approach is to start reading from the stream and assign the $i^{th}$ number in the stream a random weight uniformly at random from the interval $[0,1]$, over time keeping which ever number ends up with the largest randomly assigned value. This works because the probability the $i^{th}$ number in the stream gets the maximum value is equal to $1/n$, where $n$ is again the size of the stream. The algorithm details for this random representative sampling is shown below.

Now let us consider the correctness for the randomized number search algorithm. This algorithm chooses a representative at random, over and over, until the representative corresponds to the number $n_X$ that we are looking for, so the correctness of the algorithm is clear. Also, it is clear the space used is at most $O(\log(n))$ bits since this algorithm uses similar counter and number variables used in the naive algorithm.

The tough question then for this algorithm is, what is the runtime? This is less trivial because it is possible the random choices will be such that the algorithm never sets the representative as $n_X$, making the algorithm run forever. As before, we will model the runtime in terms of how many times we pass through the stream. On each iteration of the loop, just as in the naive algorithm, we will have $2$ passes through the stream. So to work out the runtime of the algorithm, we must answer how many iterations of the loop to expect. This is where the real fun begins!

Some Analysis

Expected Runtime

Recall that the assumption built into the problem is that there exists exactly one number that will appear in the stream at least $X$ times. This implies that when we randomly choose a representative, the probability we do choose the desired number is at least $X/n$. With this fact, we have the following result

When we consider the above, it is clear that the average performance of this algorithm improves upon the naive algorithm when $X > 1$. For those unfamiliar with randomized algorithms, there is another notable thing to internalize: the algorithm has this expected runtime for any input stream. In the deterministic case, it is simple to construct a worst case input by sticking all instances of our desired number $n_X$ at the end of the stream, forcing the algorithm to try every other number in the stream that is not $n_X$ before finding the desired number.

For this randomized scenario, however, the bad performance only occurs due to a poor random selection of representatives. Thus, the expected runtime is at most $(2/X)n$ for any input stream! Of course, the expected runtime does not take into account any variation. In fact, for all we know there is a decent chance of having a runtime much slower than the expected result! To get a clearer picture of the runtime for this algorithm, we can instead try to perform the analysis in a manner that tells us the worst case runtime with some level of confidence.

High Probability Runtime

Again recalling our desired number is in the stream at least $X$ times, this implies that at some iteration the representative chosen randomly is not the desired number with probability at most $(1 - X/n)$. Now suppose our algorithm does $k$ iterations of the main loop. Let us call $E_{k}$ the event that none of these $k$ iterations find the desired number using the randomly sampled representative. Since each iteration is independent of all others, this implies that this probability is at most

Now the above probability corresponds to a worst-case probability that our algorithm does not finish in $k$ iterations. This fact leads us to the following result

Now as we decrease $\delta$ towards $0$, our confidence of at least $1 - \delta$ is brought closer and closer to a probability of $1$ that our bound on the runtime holds true. Intuitively, smaller values for $\delta$ should force the bound on the number of times we loop over the stream to grow. The analysis validates this by having a $\log(1/\delta)$ penalty factor in the upper bound to ensure our confidence of at least $1 - \delta$. Pretty interesting! It is also interesting to note that if we choose $\delta = 1/e \approx 0.367$, we have with probability at least $0.63$ that our algorithm loops over the stream at most $(2/X)n$ times, giving us an idea how likely the average performance from earlier is!

Further, the analysis shows that if $\left(\log(1/\delta)/X\right) < 1$, then with probability at most $1 - \delta$ this algorithm has a runtime that is faster than the naive algorithm’s worst-case runtime. This is an important observation because this implies there are potentially many instances where this algorithm can out-perform the naive algorithm, in a high probability sense. For example, if we choose $\delta = 10^{-10}$, then inputs where $X \geq 24 > 10 \log(10)$ ensure with probability at least $1 - 10^{-10}$ that our runtime beats the worst-case runtime for the naive algorithm. If we look back at the average runtime bound, we know for $X > 1$ that the average performance with any input beats the naive algorithm on its worst-case input. In this high probability example, we require $X > 23$ to have that same guarantee which is certainly a bit more conservative, but the guarantee is also much stronger than in the average case since the analysis looks at the worst case runtime for some level of confidence.

Experimental Comparisons

To ground the differences between both algorithm in reality, we will showcase some experimental results based on a C++ implementation. We will see how the runtimes for both the naive and randomized algorithm play out for different values of $X$ while comparing to the predicted worst case performance when $\delta = 10^{-10}$. To enable us to do this, given some value $X$, a stream $S$ will be constructed so our desired number $n_X$ has all instances at the end of the stream. This stream constructed represents a worst-case input for the naive algorithm and so should give us a clear idea of how the naive algorithm’s worst case compares to the empirically seen worst case performance of the randomized algorithm. For the experiment, I chose to make the stream with size $n = 10^3$ and re-run the randomized algorithm $m = 10^4$ times to gather enough data to get reasonable estimates of the average and worst case performance of the randomized algorithm. The results from this experiment are shown in the below figure.

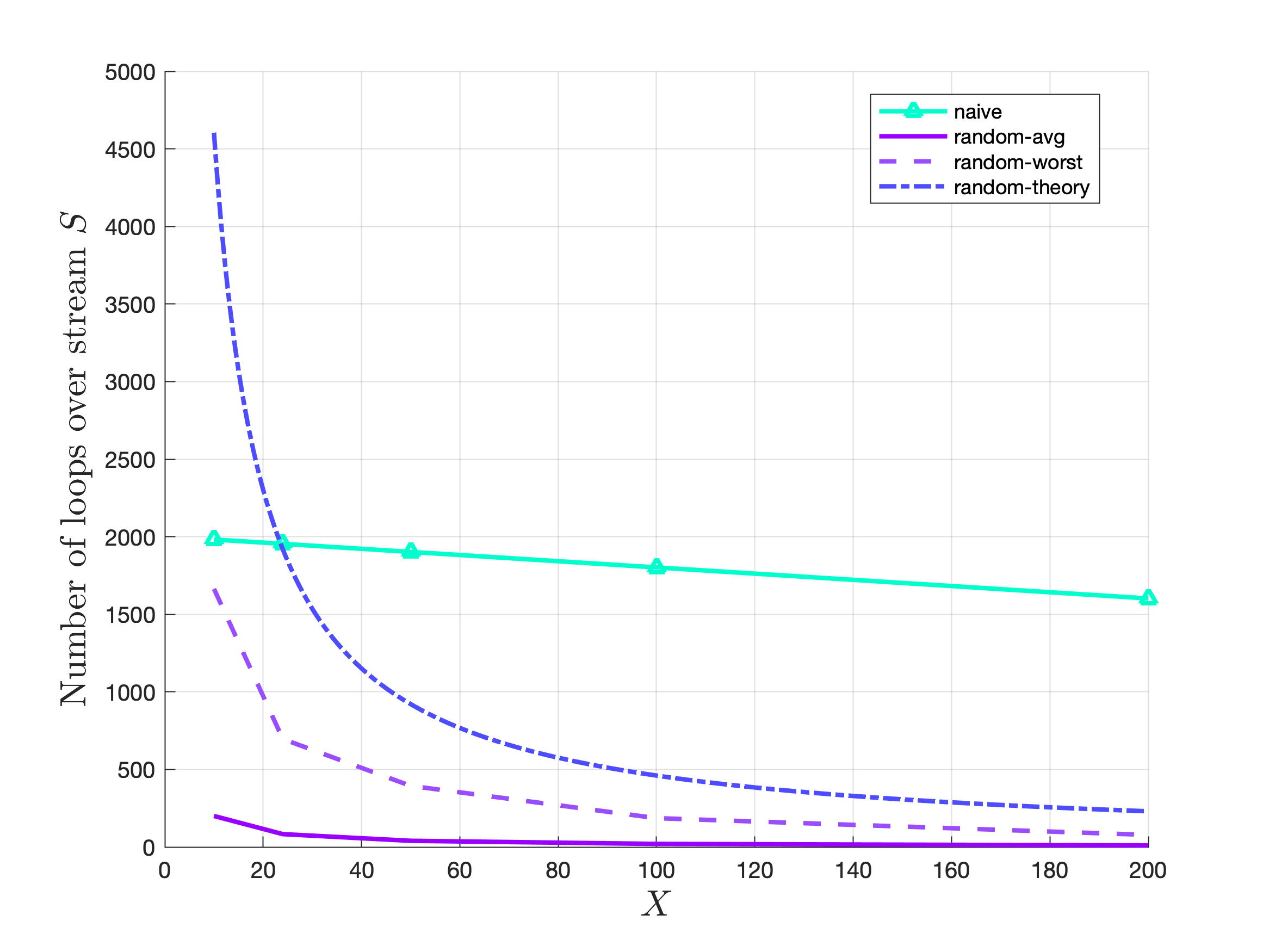
As we first glance at the results, one noticeable sight is that the performance gap between the deterministic and randomized algorithm grows as $X$ gets larger, both when looking at the average and worst case performance estimates for the randomized algorithm. This follows the results from the previous analysis since we found the randomized algorithm’s performance is inversely proportional to $X$ while the naive algorithm only has a linear decrease in $X$. Further, for $\delta = 10^{-10}$, the bound on the worst case performance for the randomized algorithm was satisfied based on the empirical results, providing credibility to the theorem about the high probability guarantees for the performance.

The full C++ implementation used to generate the data plotted above is shown below and should be compilable using C++11 on any modern operating system.

#include <stdio.h>
#include <vector>
#include <random>

namespace algo {

	class stream {
	public:

		stream() = default;
		void set_size_stream(size_t n) {
			stream_list.resize(n);
		}
		void construct_stream_only_one_with_x_instances(size_t X) {
			size_t num = 0;
			size_t cntr = 0;

			// try to populate the stream with numbers such that all numbers have at most X-1
			// instances of themselves in the array
			for(size_t i = 0; i < stream_list.size(); ++i){
				stream_list[i] = num;
				if( (++cntr) == (X-1) ){
				    ++num; cntr = 0;
				}
			}// end for i

			// populate the end of the stream with exactly X values of some number
			++num; cntr = 0;
			for(size_t i = (stream_list.size() - X); i < stream_list.size(); ++i){
				stream_list[i] = num;
			}
		}
		std::vector<size_t>::const_iterator begin() const {
			return stream_list.begin();
		}
		std::vector<size_t>::const_iterator end() const {
			return stream_list.end();
		}

	private:
		std::vector<size_t> stream_list;

	};

	// helper method to compute how often a number appears in the stream
	size_t compute_frequency_of_representative( size_t rep, const stream& s){
		size_t cntr = 0;
		for(size_t num: s){
			cntr += (rep == num);
		}// end for loop

		return cntr;
	}

	namespace naive {

		// naive algorithm's approach to selecting the ith representative
		size_t get_representative( 	size_t i, 
									const stream& s, 
									size_t* size_stream = nullptr)
		{

			// init static random engine
			size_t rep = 0;

			// use reservoir sampling to sample a representative
			// from the stream
			size_t idx = 0;
			for(size_t num: s){
				if( i == idx++ ){
				    rep = num;
				    break;
				}
			}// end for loop

			// return the representative
			return rep;
		}

		// naive algorithm for searching for a number that appears at least X times
		size_t find_number_with_atleast_X_instances( 	size_t X, 
														const stream& s, 
														size_t* num_passes = nullptr )
		{
			size_t r = 0, freq = 0;
			if( num_passes ){ *num_passes = 0; }

			// keep trying to choose the representative
			// until you find a number with at least
			// X instances in the stream
			int i = 0;
			while(freq < X){
				r = naive::get_representative(i++, s);
				freq = compute_frequency_of_representative(r, s);
				if( num_passes ){ *num_passes += 2; }
			}

			// return representative found
			return r;
		}

	}// end namespace naive

	namespace random {

		// randomized algorithm's approach to selecting a new representative
		size_t get_representative( 	const stream& s, 
									size_t* size_stream = nullptr)
		{

			// init static random engine
			static std::mt19937_64 gen;
			std::uniform_int_distribution<size_t> U;
			size_t rep = 0;

			// use reservoir sampling to sample a representative
			// from the stream
			size_t i = 0;
			for(size_t num: s){
				U = std::uniform_int_distribution<size_t>(0,i++);
				if( U(gen) == 0 ){
				    rep = num;
				}
			}// end for loop

			if( size_stream ){
				*size_stream = i;
			}

			// return the representative
			return rep;
		}

		// randomized algorithm for searching for a number that appears at least X times
		size_t find_number_with_atleast_X_instances( 	size_t X, 
														const stream& s, 
														size_t* num_passes = nullptr )
		{
			size_t r = 0, freq = 0;
			if( num_passes ){ *num_passes = 2; }

			// do a first pass to get not only the first representative,
			// but also figure out the size of the stream
			r = random::get_representative(s);
			freq = compute_frequency_of_representative(r, s);

			// keep trying to estimate the representative
			// until you find a number with at least
			// X instances in the stream
			while(freq < X){
				r = random::get_representative(s);
				freq = compute_frequency_of_representative(r, s);
				if( num_passes ){ *num_passes += 2; }
			}

			// return representative found
			return r;
		}
	}// end namespace random
}// end namespace algo

int main(int argc, char** argv){
    
	// the value X representing the minimum number
	// of times our desired number appears in the
	// stream and the strict upper bound on how
	// many times any other number appears
	size_t X = 24;

	// construct the stream with a worst case input
	// for the deterministic algorithm
	algo::stream s;
	s.set_size_stream(1000);
	s.construct_stream_only_one_with_x_instances(X);

	// init temporary variable for retrieving the
	// number of times we loop over the stream
	// before we find the desired number
	size_t num_passes = 0;

	// naive runtime
	std::cout << "|Naive algorithm performance|" << std::endl;
	auto number_naive   = algo::naive::find_number_with_atleast_X_instances(X, 
																			s, 
																			&num_passes);
	std::cout 	<< "Found " << number_naive << " in " 
				<< num_passes << " passes of the stream" << std::endl;

	// random runtime
	std::cout << std::endl;
	std::cout << "|Randomized algorithm performance|" << std::endl;
	size_t num_runs = 10000;
	size_t avg = 0, worst = 0, number_rand = 0;
	for(size_t i = 0; i < num_runs; ++i){
	    number_rand = algo::random::find_number_with_atleast_X_instances(	X, 
																			s, 
																			&num_passes);
	    worst = std::max(worst, num_passes);
	    avg += num_passes;
	}
	avg /= num_runs;
	std::cout 	<< "Found " << number_rand << " in an (average, max) number of (" 
				<< avg << ", " << worst << ") passes of the stream" << std::endl;

	return 0;
}

Conclusion

Within this post, we went over some basic concepts behind streaming algorithms and illustrated them through a search problem related to streams. We saw that while deterministic algorithms can be quite simple in the streaming context, sometimes using a bit of randomness can take us a lot further to solving a streaming problem efficiently. We also saw that while the deterministic algorithm had very simple analysis, it can take a bit of mathematical elbow grease to properly understand what randomized algorithms can and cannot do for us. When it comes to streaming, there are many more interesting problems to discover, so I recommend those interested go take a look and explore this deep and interesting area!